Teorie grup
Teorie grup je matematická disciplína zabývající se studiem grup. Jde o podobor algebry. Má mnoho aplikací v celé matematice i v dalších oborech – fyzice, informatice či chemii.
Historie[editovat | editovat zdroj]
Počátky teorie grup sahají do posledních let 18. a počátku 19. století, kdy se začala vyvíjet jako důsledek rozvoje teorie algebraických rovnic, teorie čísel a geometrie. Prvními matematiky, kteří se zabývali touto oblastí byli Leonhard Euler, Joseph Louis Lagrange, Carl Friedrich Gauss, Niels Henrik Abel a Évariste Galois.
Moderní definici grupy podal roku 1882 Walther von Dyck.
| Tato část článku je příliš stručná nebo neobsahuje všechny důležité informace. Pomozte Wikipedii tím, že ji vhodně rozšíříte. |
Grupa[editovat | editovat zdroj]
- Související informace naleznete také v článku Grupa.
Grupa je základním pojmem teorie grup. Je definována jako množina  spolu s binární operací
spolu s binární operací  splňující tři grupové axiomy:
splňující tři grupové axiomy:
-
Asociativita: 
Existence neutrálního prvku: 
Existence inverzních prvků: 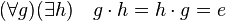
Důležité věty teorie grup[editovat | editovat zdroj]
- Lagrangeova věta: Je-li G konečná grupa a H její podgrupa, pak řád H dělí řád G.
- Cayleyho věta: Každá grupa G je izomorfní podgrupě grupy permutací na G (symetrické grupě).
- Sylowovy věty: Popisují existenci a vlastnosti p-podgrup konečné grupy.
- Věta o homomorfismu: Dává do souvislosti dvě grupy, mezi nimiž je homomorfismus, s jeho jádrem a obrazem.
- Jordan-Hölderova věta: Každé dvě kompoziční řady dané grupy jsou izomorfní.
- Krull-Schmidtova věta: Stanovuje podmínky pro to, aby grupa G byla konečným součinem svých nerozložitelných podgrup.
- Burnsidovo lemma: Počet orbit akce grupy na množinu se rovná průměrnému počtu bodů fixovaných jednotlivými prvky grupy.
- Klasifikace konečně generovaných abelovských grup: Každá konečně generovaná abelovská grupa je jednoznačně vyjádřitelná jako direktní suma cyklických grup řádu nekonečného nebo mocniny prvočísla.
- Klasifikace konečných jednoduchých grup: Jeden z vrcholných výsledků matematiky 20. století.
