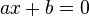Termín lineární rovnice v matematice označuje algebraickou rovnici prvního stupně, tzn. rovnici o jedné neznámé, ve které neznámá vystupuje pouze v první mocnině. V základním tvaru vypadá následovně:
Lineární rovnice je taková rovnice, kterou můžeme upravit na tvar ax + b = 0, kde a≠0. Konkrétní příklad by mohl vypadat třeba takto: 2x + 4 = 0. Řešením této rovnice je číslo −2, což se dá asi docela logicky vydedukovat. Pokud by tam byly trochu větší čísla, už by ona dedukce nebyla tak jednoduchá, takže to bude chtít nějaký konkrétnější postup.
Základní tvar lineární rovnice
Lineární rovnice je rovnice, která obsahuje jednu neznámou x, která není nijakumocněna, odmocněna apod. Prohlédněte si příklady různých lineárních rovnic:
Jak vidíte, lineární rovnice může mít mnoho různých tvarů. Abychom mohli lineární rovnice nějak hezky řešit, potřebujeme je upravit na základní tvar. Základní tvar lineární rovnice vypadá takto:
kde x je neznámá a symboly a a b jsou libovolná reálná čísla. Přitom číslo a nesmí být nulové, tj. a≠0. Výrazu ax říkáme lineární člen, výrazu b říkáme absolutní člen.
Při výpočtu lineární rovnice můžeme použít mnoho různých ekvivalentních úprav(to jest takové úpravy, které nezmění výsledek rovnice). Tyto úpravy je nutné znát, bez nich není možné nějakou složitější rovnici řešit. Upravit rovnici na základní tvar můžeme buď úpravou samotných výrazů, které se v rovnici vyskytují nebo můžeme použítekvivalentní úpravy rovnic.
Z předchozích příkladů: rovnice 2x + 7 = 0 už je v základním tvaru a platí, že a = 2 a b = 7. Druhá rovnice, x − 2 = 74 není v základním tvaru. Použijeme ekvivalentní úpravu a k oběma stranám rovnice přičteme číslo −74 (neboli od obou stran odečteme číslo 74). Dostaneme rovnici x − 76 = 0. Tato rovnice už je v základním tvaru a platí a= 1 a b = −76.
Předposlední rovnice má do základního tvaru daleko, ale i tu můžeme vhodně upravit. Nejprve „vyrobíme“ na pravé straně nulu. Přičteme tak k rovnici výraz 12x. Pravou stranu tím vynulujeme, protože (−12x)+12x = 0. Celá rovnice bude vypadat takto:
Teď už nám zbývá jen sečíst závorky.
Tato lineární rovnice je v základním tvaru a platí, že a = −8 a b = 3.
V poslední rovnici se musíme jednak zbavit zlomků a také musíme odstranit x2, protože takový výraz v lineární rovnici být nemůže. Zlomek x2x ale můžeme jednoduše pokrátit jen na výraz x. Dostaneme tak rovnici
Zlomků se zbavíme tak, že celou rovnici vynásobíme 72:
Zkrátíme:
A tuto rovnici už jednoduše převedeme na lineární rovnici, tak že převedeme všechny výrazy na levou stranu a sečteme:
Platí, že a = −438 a b = 0.
Jak řešit lineární rovnici
Máme-li lineární rovnici v základním tvaru, tak už se řeší snadno. Ukažme si to na příkladu: 3x − 18 = 0. Od čeho musíme odečíst číslo 18, abychom dostali nulu? No zase od čísla 18. Takže aby se výraz 3x − 18 rovnal nule, musí se výraz 3x rovnat 18, pak dostaneme 18 − 18 = 0. Kdy se bude výraz 3x rovnat 18? Právě když platí, že x= 6, protože 3 · 6 = 18.
Jak z toho odvodíme obecný postup? Jako první musíme zjistit, čemu se má rovnat lineární člen ax. To zjistíme tak, že převedeme absolutní člen na pravou stranu rovnice, tj. k rovnici přičteme −b. Tím získáme rovnici ve tvaru ax + b−b = −b, což je totéž jako ax = −b. V případě předchozího příkladu bychom tak dostali 3x + 18 − 18 = 18, tedy 3x = 18. Nezapomeňte, že číslo b bylo rovno b = −18, takže pokud přičítáme−b, přičítáme −(−18) a to je rovno +18.
Rovnici máme ve tvaru ax = −b. Jakým způsobem získáme přímo x? V příkladu jsme hledali takové x, které když vynásobíme třemi, tak získáme 18. Co jsme ve skutečnosti dělali? Vydělili jsme 18/3 = 6. Tedy vzali jsme výraz na pravé straně (−b) a vydělili jsme ho hodnotou a, v příkladu trojkou. Takže z ax = −b dostaneme
Celý postup aplikovaný na první příklad vypadá takto:
Ukázka příkladu číslo 2.
Řešte v Q rovnici:
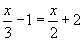
Řešení:
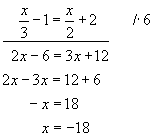
Zkouška:
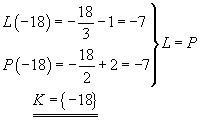
Ukázka příkladu číslo 7.
Řešte rovnici v Z:
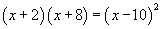
Řešení:
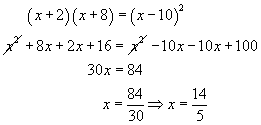
Zkouška:
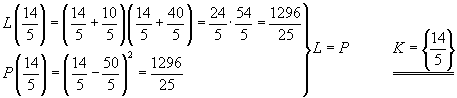
Ukázka příkladu číslo 13.
Řešte v R rovnici:
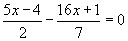
Řešení:
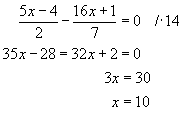
Zkouška:
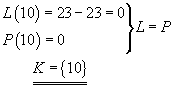
Lineární rovnice je matematický zápis, který můžeme (za pomoci ekvivalentních úprav) upravit na tvar
ax + b = 0.
x … neznámá; při řešení rovnice ji určujeme (vyskytuje se pouze v první mocnině, tedy ne na druhou, na třetí, na jednu polovinu atd.)
a, b … libovolná reálná čísla
Ekvivalentní úpravy jsou takové úpravy, které nemění výsledek rovnice. Při použití neekvivalentních úprav (například umocňování) může dojít ke změně výsledku rovnice, a proto je nutné provést zkoušku (viz dále).
Reálné číslo je takové číslo, které můžeme zobrazit na číselné ose.
Je zápis 2x + 5 = 0 lineární rovnice?
Na první pohled vidíme, že ano.
x … neznámá, a = 2 (reálné číslo), b = 5 (reálné číslo)
A jaké má rovnice řešení?
Abychom rovnici vyřešili, musímě určit hodnotu neznámé x.
Rovnici upravíme tak, že členy s x (v této rovnici se jedná o člen 2x) necháme na jedné straně rovnice a ostatní členy (v této rovnici číslo 5) převedeme na stranu druhou:
2x = −5
Převedením čísla 5 na druhou stranu rovnice se změní jeho znaménko.
Při převodu členů z jedné strany rovnice na druhou se mění znaménka + na –(a opačně) a ∙ na : (a opačně).
Na levé straně rovnice máme člen 2x. Nás však zajímá, kolik se rovná x. Převedeme tedy dvojku také na druhou stranu rovnice. Jelikož na levé straně dvojkou neznámou x násobíme, po převedení na pravou stranu, budeme dvojkou dělit. Celou rovnici (levou a i pravou stranu) vlastně dělíme dvěma.
Výsledek tedy je:

Obecný zápis řešení lineární rovnice je x = −b/a , za podmínky, že a ≠ 0. Nulou totiž dělit nelze. Pokud si do uvedené rovnice dosadíme za a nulu, zjistíme, že takový zápis nedává smysl.
A co zápis 2x − 6 = 0? Je lineární rovnicí?
Již víme, že obecný zápis lineární rovnice je ax + b = 0, avšak v dané rovnici je −6. Ale i tato rovnice je lineární, jelikož odčítání je vlastně přičítání záporného čísla. Můžeme tak psát2x + (−6) = 0. Plus a mínus dává totiž mínus a rovnice se tak nemění. Uvedená rovnice je tedy lineární. Řešení tentokrát nechám na Vás. ![]()
Lineární rovnice s neznámou ve jmenovateli
Společně si zkusíme vyřešit následující rovnici:
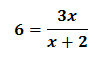
Pokud se neznámá vyskytuje ve jmenovateli, musíme nejprve stanovit tzv. podmínky řešitelnosti. To jsou takové podmínky, za kterých má daný výraz smysl.
Náš výraz by neměl smysl, pokud by se jmenovatel rovnal nule – kdyby platilo x + 2 = 0. Na první pohled je vidět, že tento výraz (jedná se vlastně taky o lineární rovnici) je roven nule, když x = −2. Aby tedy rovnice měla smysl, x ≠ −2. To je podmínka řešitelnosti.
Nyní přejdeme k samotnému řešení rovnice.
Nejprve se zbavíme zlomku na pravé straně tak, že jmenovatel x + 2 převedeme na levou stanu rovnice. Jelikož na pravé straně rovnice výrazem x + 2 dělíme, po přesunutí na stranu pravou, jím budeme násobit (celou rovnici vlastně vynásobíme výrazem x + 2):
6 ∙ (x + 2) = 3x
Závorku roznásobíme (číslem 6 vynásobíme každý člen v závorce):
6x + 12 = 3x
3 x + 12 = 0 (z tohoto tvaru vidíme, že se jedná o lineární rovnici ve tvaru ax + b = 0)
3x = −12
x = −12/3
x = −4
Vidíme, že výsledek není v rozporu s podmínkou řešitelnosti a tudíž řešením rovnice je číslo −4.
Neekvivalentní úpravy a zkouška
Pokud při úpravě rovnic provádíme tzv. neekvivalentní úpravy (umocňování), je třeba provést zkoušku.
Rovnice:
![]()
Dále ji upravíme:
x − 1 = 1 (obě strany jsme umocnili na druhou, což ale je neekvivalentní úprava)
x = 2
Dostali jsme výsledek, avšak jelikož jsme provedli neekvivalentní úpravu, je potřeba provést zkoušku. Dosadíme tedy výsledek nejprve do pravé strany rovnice, a pak porovnáme s levou stranou rovnice.
Zk.:

Ze zkoušky tak vidíme, že rovnice nemá řešení. To, že rovnice nemá řešení, je však vidět na první pohled, jelikož výraz pod odmocninou nemůže být záporný.
Rovnice navíc není lineární. Sice lze upravit na tvar x − 2 = 0, což odpovídá obecnému zápisu lineární rovnice ax + b = 0, avšak takto ji upravíme pomocí neekvivalentních úprav.
Pokud si nejsme jisti, zda jsme provedli či neprovedli během úpravy rovnice neekvivalentní úpravu, je dobré provést zkoušku, abychom si výpočet ověřili.
Užití rovnic
Podívejme se na následující úlohu:
Lahev s pitím stojí 50 Kč. Pití je o 40 Kč dražší než prázdná lahev. Kolik stojí samotná lahev.
I když to může na první pohled svádět, že lahev stojí 10 Kč, není tomu tak.
Označme cenu lahve písmenem l. (Pro neznámou můžeme použít libovolné písmeno. V abecedě máme totiž i jiná písmena než x.)
Ze zadání víme, že cena pití je o 40 korun vyšší. K ceně lahve l je tedy potřeba přičíst 40 Kč, abychom dostali cenu samotného pití. Tedy cena samotného pití je l + 40 (Kč).
Máme tedy:
l … cena lahve
l + 40 (Kč) … cena samotného pití (bez lahve)
Cena lahve s pitím je 50 Kč. Rovnici tedy sestavíme následovně:
l + l + 40 = 50
Rovnici dále řešíme:
2l + 40 = 50
2l = 10
l = 5 (Kč)
Cena lahve je 5 Kč.
Dovolené úpravy rovnice (ekvivalentní úpravy rovnice):