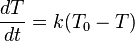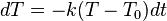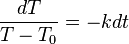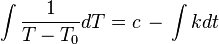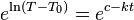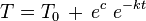Diferenciální rovnice je matematická rovnice, ve které jako proměnné vystupují derivace funkcí. Diferenciální rovnice stojí v základech fyziky a jejich aplikace najdeme ve většině oblastí lidského vědění.

Matematická teorie diferenciálních rovnic se zabývá existencí řešení, jednoznačností (čili zda je řešení jen jedno), závislostí řešení na počátečních a okrajových podmínkách.

Ve fyzice a dalších aplikacích je zajímavé zejména získání analytického řešení, tedy funkce u(t), která rovnici řeší. Pokud taková funkce nejde analyticky vyjádřit, vstupuje do hry numerické řešení diferenciálních rovnic.

 

 

Typy diferenciálních rovnic[editovat | editovat zdroj]

Základní dělení diferenciálních rovnic je podle typu obsažených derivací:

• Obyčejné diferenciální rovnice (ODR): obsahují derivace hledané funkce jen podle jedné proměnné.
• Parciální diferenciální rovnice (PDR): obsahují derivace hledané funkce podle více proměnných, tedy parciální derivace.

Pokud je dáno  diferenciálních rovnic pro  neznámých funkcí, pak hovoříme o soustavě diferenciálních rovnic.
Řád diferenciální rovnice je řád nejvyšší derivace, která je v ní obsažená. Za řád soustavy diferenciálních rovnic považujeme hodnotu nejvyšší derivace, která se v soustavě vyskytuje. Podle řádu bývají diferenciální rovnice děleny na diferenciální rovnice prvního řádua diferenciální rovnice vyšších řádů.

Diferenciální rovnice, v nichž se hledaná funkce vyskytuje pouze lineárně, přičemž se nikde nevyskytují ani součiny hledané funkce s jejími derivacemi, ani součiny derivací této funkce, označujeme jako lineární diferenciální rovnice. Pokud jedna z uvedených podmínek není splněna, hovoříme o nelineárních diferenciálních rovnicích.

Řešení rovnice[editovat | editovat zdroj]

Za řešení (integrál) diferenciální rovnice (v daném oboru) považujeme každou funkci, která má příslušné derivace a vyhovuje dané diferenciální rovnici. Řešením (integrálem) soustavy diferenciálních rovnic je množina funkcí s derivacemi potřebného řádu, které vyhovují všem rovnicím dané soustavy.

Řešení diferenciálních rovnic dělíme na

• obecné – Jako obecné řešení označujeme takové řešení diferenciální rovnice, které obsahuje libovolnou integrační konstantu. Přiřadíme-li každé konstantě obecného řešení určitou číselnou hodnotu, získáme řešení partikulární.
• partikulární (částečné) – Partikulární (částečné) řešení je řešení diferenciální rovnice, které získáme přiřazením určité číselné hodnoty každé integrační konstantě obecného řešení.
• singulární (výjimečné) – Některá řešení nelze získat z obecného řešení. Taková řešení, která se vyskytují pouze u některých rovnic, popř. v některých bodech oboru, označujeme jako singulární nebo výjimečná.

Partikulární řešení můžeme v případě jednoduchých diferenciálních rovnic vypočítat analyticky. Nicméně ve velkém množství případů je analytické řešení příliš obtížné a diferenciální rovnice se řeší numericky.

Příklad[editovat | editovat zdroj]

Stojí-li v místnosti sklenice s horkým čajem, ubývá z ní teplo rychlostí, která je přímo úměrná rozdílu mezi teplotou čaje  a teplotou v místnosti  (kterou pro jednoduchost pokládejme za konstantní). Koeficient této úměrnosti značme . Máme tedy diferenciální rovnici

a chceme najít všechny funkce  (závislost teploty na čase), které ji splňují.

Tato rovnice je tedy podle výše uvedené klasifikace obyčejná diferenciální rovnice 1. řádu

Řešení příkladu[editovat | editovat zdroj]

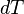 lze chápat jako diferenciál, tedy funkci dvou proměnných 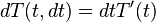. Zlomek  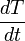v tomto významu se rovná derivaci  podle  (proto se derivace takto značí). Díky tomu lze uvedenou rovnici upravit:

Strany rovnice se rovnají, právě když se rovnají jejich neurčité integrály (rozdíl obou integračních konstant označme ).

Vypočtením těchto integrálů obdržíme

Strany se rovnají, právě když se rovnají jejich exponenciály. Pro názornost předpokládejme :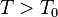

To lze upravit na

Tato diferenciální rovnice má tedy nekonečně mnoho řešení, přičemž různé hodnoty c odpovídají různým funkcím T(t), které popisují chladnutí čaje s různou počáteční teplotou.